What is Total Internal Reflection? Definition, Conditions, Formula, Diagram, Advantages, Applications & Disadvantages

Total Internal Reflection is an optical phenomenon that occurs when a wave traveling in a denser medium (higher refractive index) strikes the boundary of a less dense medium (lower refractive index) at an angle greater than the critical angle, leading to complete reflection of the wave within the denser medium.

Conditions for Total Internal Reflection

For Total Internal Reflection to take place, two conditions must be met:

1. The incident ray must travel from a denser medium to a rarer medium (i.e., from a medium of higher refractive index to a medium of lower refractive index, such as from glass to air or water to air).
2. The angle of incidence must be greater than the critical angle (\(\theta_c\)) for the given pair of media.

Diagram Representation of Total Internal Reflection

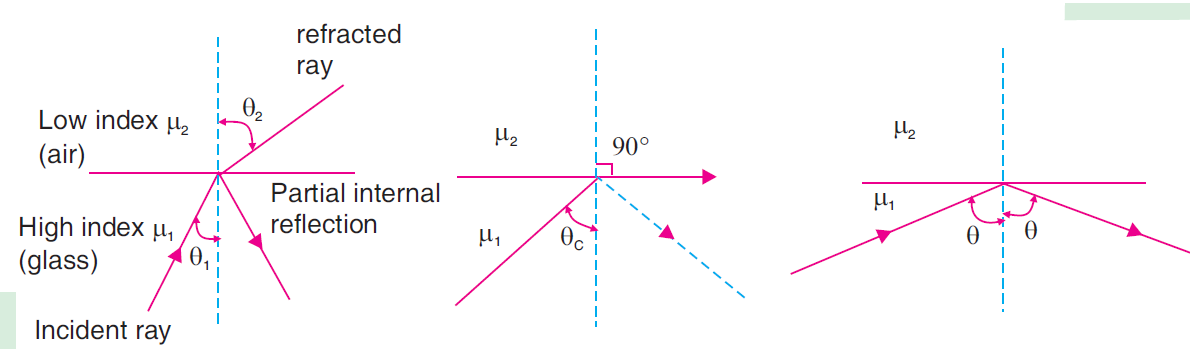
A typical diagram illustrating Total Internal Reflection includes:

1. An incident ray traveling from a denser medium (glass, water) to a rarer medium (air).
2. The critical angle (\(\theta_c\)) and the refracted ray traveling along the boundary when \(\theta_1\) = \(\theta_c\).
3. Total internal reflection occurring when \(\theta_1\) > \(\theta_c\).

Critical Angle (\(\theta_c\)) and Formula

The critical angle is the angle of incidence beyond which total internal reflection occurs. It can be calculated using Snell’s law:

\[
\mu_1 \sin \theta_1 = \mu_2 \sin \theta_2
\]

where:
\( \mu_1 \) = refractive index of the denser medium
\( \mu_2 \) = refractive index of the rarer medium
\( \theta_1 \) = angle of incidence
\( \theta_2 \) = angle of refraction

For the critical angle (\(\theta_c\)), \( \theta_2 = 90^\circ \), so:

\[
\sin \theta_c = \frac{\mu_2}{\mu_1}
\]

Examples of Total Internal Reflection

1. Mirage Formation: The bending of light due to temperature differences causes mirages in deserts and on hot roads.
2. Diamond Sparkle: Diamonds have a high refractive index (~2.42), leading to Total Internal Reflection and enhancing their brilliance.
3. Optical Fibers: Light signals in optical fibers undergo repeated Total Internal Reflection, allowing data transmission over long distances with minimal loss.
4. Prisms in Binoculars: Prisms in binoculars use Total Internal Reflection to reflect light multiple times, making them compact and efficient.
5. Light Pipes: Used in architectural lighting and medical endoscopes to direct light efficiently.

Advantages of Total Internal Reflection

1. High Efficiency: No loss of energy due to refraction, making it ideal for optical fibers and communication.
2. Enhances Brightness: Used in diamond cutting to maximize brilliance.
3. Clearer Imaging: Used in high-quality optical instruments like periscopes and endoscopes.
4. No Light Absorption: Unlike mirrors, which absorb some light, Total Internal Reflection ensures maximum reflection without losses.

Applications of Total Internal Reflection

1. Fiber Optic Communication: Used in telecommunication and medical imaging (endoscopy).
2. Periscopes & Binoculars: Utilized in military and submarine periscopes for superior imaging.
3. Diamond Industry: Cut to optimize Total Internal Reflection for enhanced sparkle.
4. Rain Sensors in Cars: Uses Total Internal Reflection to detect water droplets on windshields.
5. Light Guides in Architecture: Used to distribute natural light efficiently in buildings.

Disadvantages of Total Internal Reflection

1. Limited to Certain Angles: Total Internal Reflection occurs only when the angle of incidence exceeds the critical angle.
2. Dependent on Refractive Index: Requires a significant difference in refractive indices between media.
3. Potential Signal Loss in Fiber Optics: Impurities and bending beyond a critical radius can cause signal loss.
4. Material Limitations: Requires specific materials with high refractive indices for optimal results.

Conclusion

Total Internal Reflection is a fundamental optical principle with significant applications in modern technology, particularly in fiber optics, optical instruments, and imaging systems. Its advantages in high-efficiency light transmission and imaging make it indispensable in various industries, though careful considerations of refractive indices and angles are essential for effective utilization.