An inclined manometer is a device used to measure small pressure differences with greater accuracy. It consists of an inclined tube filled with a liquid, allowing for more precise readings compared to a standard U-tube manometer.
Construction of Inclined Manometer
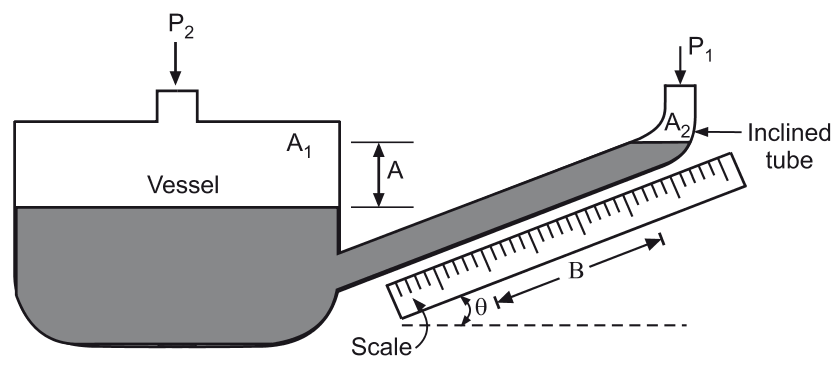
A typical inclined manometer consists of:
- Vessel or Reservoir – Holds the liquid and connects to one pressure source.
- Inclined Tube – A transparent, inclined tube for precise measurement.
- Manometric Liquid – Commonly water, mercury, or oil.
- Scale – A graduated scale aligned with the inclined tube to measure displacement.
- Connections to Pressure Points – Ports for measuring pressures \( P_1 \) and \( P_2 \).
- Angle of Inclination (θ) – The inclination angle enhances measurement sensitivity.
Working Principle of Inclined Manometer
The inclined manometer works on the principle of hydrostatic pressure balance. The pressure difference is determined by measuring the liquid displacement along the inclined tube, where a small vertical pressure change results in a larger horizontal movement of the liquid.
Derivation of Inclined Manometer Equation
Let:
\( P_1 \) = Pressure at point 1
\( P_2 \) = Pressure at point 2
\( h \) = Vertical height difference
\( B \) = Length of liquid column along the inclined tube
\( \theta \) = Angle of inclination
\( \rho \) = Density of the manometric liquid
\( g \) = Acceleration due to gravity
\( A_1 \) = Cross-sectional area of the reservoir
\( A_2 \) = Cross-sectional area of the inclined tube
Hydrostatic Pressure Balance
From the fundamental equation of hydrostatics:
\[P_1 – P_2 = \rho g h\]
Since the vertical height \( h \) is related to the inclined tube length \( B \) by:
\[h = B \sin \theta\]
Substituting \( h \) into the pressure equation:
\[\Delta P = P_1 – P_2 = \rho g B \sin \theta\]
Considering Cross-Sectional Area, the volume displacement relationship is:
\[A_1 h = A_2 B\]
Substituting \( h = B \sin \theta \):
\[A_1 (B \sin \theta) = A_2 B\]
Solving for \( B \):
\[B = \frac{A_1}{A_2} h = \frac{A_1}{A_2} B \sin \theta\]
Final Equation
Thus, incorporating area considerations into the pressure equation:
\[\Delta P = \rho g \frac{A_1}{A_2} B \sin \theta\]
This equation demonstrates how the inclined tube increases the effective measurement length \( B \), improving sensitivity while considering volume displacement effects.
Advantages of Inclined Manometer
- Greater sensitivity for small pressure differences.
- More accurate than vertical manometers.
- Simple construction and easy to use.
- Requires no external power.
- Can measure both positive and negative pressures.
Applications of Inclined Manometer
- Measuring low-pressure differentials in HVAC systems.
- Used in laboratories for fluid mechanics studies.
- Calibration of pressure-sensitive instruments.
- Monitoring gas flow and air pressure variations.
- Industrial applications where precise pressure measurements are required.
Disadvantages of Inclined Manometer
- Not suitable for very high pressures.
- Requires careful alignment for accuracy.
- Manometric liquid must be carefully chosen to avoid evaporation or contamination.
- Can be affected by temperature variations.
Conclusion
The inclined manometer is a highly sensitive and precise instrument for measuring small pressure differences. Its inclined tube design enhances accuracy, making it invaluable for scientific and industrial applications requiring precise pressure monitoring.
